Pola bilangan, sebuah konsep fundamental dalam matematika, hadir di mana-mana dalam kehidupan sehari-hari. Mulai dari susunan daun pada batang pohon, pola keramik di lantai, hingga deret angka dalam sebuah jadwal, semuanya menunjukkan adanya keteraturan yang dapat diprediksi. Di jenjang Sekolah Menengah Pertama (SMP), khususnya kelas 8 semester 1, pemahaman tentang pola bilangan menjadi krusial sebagai fondasi untuk materi matematika yang lebih kompleks di masa depan.
Artikel ini akan membawa Anda menyelami lebih dalam tentang pola bilangan melalui berbagai contoh soal yang relevan untuk siswa kelas 8 semester 1. Kita akan membahas berbagai jenis pola, strategi penyelesaiannya, serta tips untuk menguasai materi ini dengan baik.
Memahami Konsep Dasar Pola Bilangan
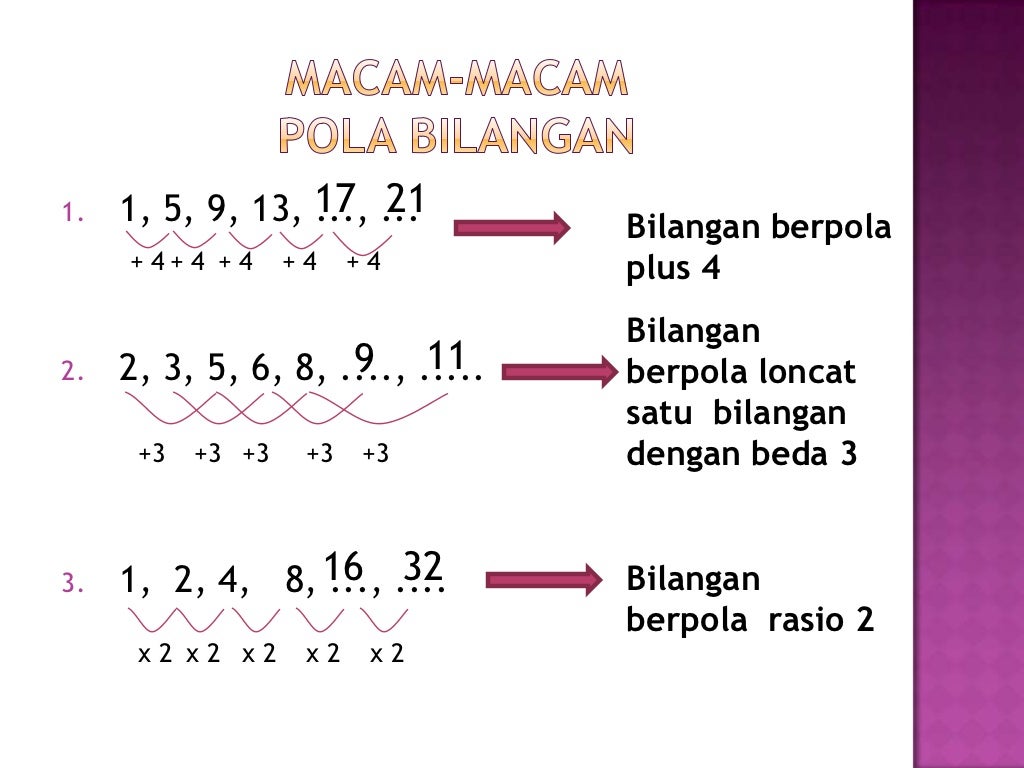
Sebelum kita melangkah ke contoh soal, mari kita samakan persepsi tentang apa itu pola bilangan. Pola bilangan adalah susunan bilangan yang memiliki aturan atau cara tertentu dalam pembentukannya. Aturan ini bisa berupa penambahan, pengurangan, perkalian, pembagian, atau kombinasi dari operasi-operasi tersebut, bahkan bisa juga melibatkan pangkat atau akar. Kunci untuk memahami pola bilangan adalah mengidentifikasi keteraturan yang ada di antara suku-suku bilangan tersebut.
Dalam konteks kelas 8 semester 1, kita biasanya akan berhadapan dengan:
- Pola Aritmetika: Pola di mana selisih antara dua suku berurutan selalu konstan. Selisih ini disebut beda (b).
- Pola Geometri: Pola di mana hasil bagi antara dua suku berurutan selalu konstan. Hasil bagi ini disebut rasio (r).
- Pola Bilangan Khusus: Pola yang tidak selalu mengikuti aturan aritmetika atau geometri murni, tetapi memiliki ciri khas tersendiri (misalnya pola bilangan persegi, pola bilangan segitiga, pola Fibonacci, dll.).
Contoh Soal dan Strategi Penyelesaiannya
Mari kita mulai dengan berbagai contoh soal yang sering muncul dalam ujian maupun latihan di kelas 8 semester 1.
Contoh Soal 1: Pola Aritmetika Sederhana
Perhatikan barisan bilangan berikut: 3, 7, 11, 15, …
Tentukan:
a. Suku ke-5 dan suku ke-6.
b. Rumus suku ke-n (Un).
c. Suku ke-20.
Analisis dan Strategi Penyelesaian:
-
Mengidentifikasi Jenis Pola:
- Perhatikan selisih antara suku-suku berurutan:
- 7 – 3 = 4
- 11 – 7 = 4
- 15 – 11 = 4
- Karena selisihnya konstan (yaitu 4), maka ini adalah pola aritmetika.
- Suku pertama (U1) = 3.
- Beda (b) = 4.
- Perhatikan selisih antara suku-suku berurutan:
-
Menentukan Suku ke-5 dan Suku ke-6 (Bagian a):
- Untuk mencari suku selanjutnya, kita cukup menambahkan beda ke suku sebelumnya.
- Suku ke-5 (U5) = Suku ke-4 (U4) + b = 15 + 4 = 19.
- Suku ke-6 (U6) = Suku ke-5 (U5) + b = 19 + 4 = 23.
-
Menentukan Rumus Suku ke-n (Bagian b):
- Rumus umum suku ke-n untuk barisan aritmetika adalah:
Un = a + (n-1)baadalah suku pertama.nadalah nomor suku yang ingin dicari.badalah beda.
- Dalam kasus ini,
a = 3danb = 4. - Jadi, rumusnya adalah:
Un = 3 + (n-1)4 - Kita bisa sederhanakan:
Un = 3 + 4n - 4 Un = 4n - 1
- Rumus umum suku ke-n untuk barisan aritmetika adalah:
-
Menentukan Suku ke-20 (Bagian c):
- Sekarang kita gunakan rumus suku ke-n yang sudah kita temukan:
Un = 4n - 1. - Untuk mencari suku ke-20, substitusikan
n = 20. - U20 = 4(20) – 1
- U20 = 80 – 1
- U20 = 79.
- Sekarang kita gunakan rumus suku ke-n yang sudah kita temukan:
Jawaban Soal 1:
a. Suku ke-5 adalah 19, suku ke-6 adalah 23.
b. Rumus suku ke-n adalah Un = 4n - 1.
c. Suku ke-20 adalah 79.
Contoh Soal 2: Pola Geometri Sederhana
Perhatikan barisan bilangan berikut: 2, 6, 18, 54, …
Tentukan:
a. Suku ke-5 dan suku ke-6.
b. Rumus suku ke-n (Un).
c. Suku ke-7.
Analisis dan Strategi Penyelesaian:
-
Mengidentifikasi Jenis Pola:
- Perhatikan hasil bagi antara suku-suku berurutan:
- 6 / 2 = 3
- 18 / 6 = 3
- 54 / 18 = 3
- Karena hasil baginya konstan (yaitu 3), maka ini adalah pola geometri.
- Suku pertama (a) = 2.
- Rasio (r) = 3.
- Perhatikan hasil bagi antara suku-suku berurutan:
-
Menentukan Suku ke-5 dan Suku ke-6 (Bagian a):
- Untuk mencari suku selanjutnya, kita cukup mengalikan suku sebelumnya dengan rasio.
- Suku ke-5 (U5) = Suku ke-4 (U4) × r = 54 × 3 = 162.
- Suku ke-6 (U6) = Suku ke-5 (U5) × r = 162 × 3 = 486.
-
Menentukan Rumus Suku ke-n (Bagian b):
- Rumus umum suku ke-n untuk barisan geometri adalah:
Un = a * r^(n-1)aadalah suku pertama.nadalah nomor suku yang ingin dicari.radalah rasio.
- Dalam kasus ini,
a = 2danr = 3. - Jadi, rumusnya adalah:
Un = 2 * 3^(n-1).
- Rumus umum suku ke-n untuk barisan geometri adalah:
-
Menentukan Suku ke-7 (Bagian c):
- Gunakan rumus suku ke-n:
Un = 2 * 3^(n-1). - Untuk mencari suku ke-7, substitusikan
n = 7. - U7 = 2 * 3^(7-1)
- U7 = 2 * 3^6
- U7 = 2 * (729)
- U7 = 1458.
- Gunakan rumus suku ke-n:
Jawaban Soal 2:
a. Suku ke-5 adalah 162, suku ke-6 adalah 486.
b. Rumus suku ke-n adalah Un = 2 * 3^(n-1).
c. Suku ke-7 adalah 1458.
Contoh Soal 3: Pola Bilangan Khusus (Pola Bilangan Persegi)
Perhatikan susunan titik-titik berikut:
- Suku 1: * (1 titik)
- Suku 2:
- *
-
- (4 titik)
- Suku 3:
-
-
- (9 titik)
-
-
- Suku 4:
-
-
-
- (16 titik)
-
-
-
Tentukan:
a. Jumlah titik pada suku ke-5.
b. Rumus suku ke-n (Un) untuk jumlah titik.
c. Jumlah titik pada suku ke-10.
Analisis dan Strategi Penyelesaian:
-
Mengidentifikasi Pola:
- Jumlah titik pada setiap suku adalah: 1, 4, 9, 16, …
- Perhatikan keteraturan jumlah titik ini:
- 1 = 1²
- 4 = 2²
- 9 = 3²
- 16 = 4²
- Ternyata, jumlah titik pada suku ke-n adalah n kuadrat. Ini adalah pola bilangan persegi.
-
Menentukan Jumlah Titik pada Suku ke-5 (Bagian a):
- Karena rumusnya adalah
Un = n², maka untuk suku ke-5, kita substitusikann = 5. - U5 = 5² = 25.
- Karena rumusnya adalah
-
Menentukan Rumus Suku ke-n (Bagian b):
- Berdasarkan analisis, rumus suku ke-n untuk jumlah titik adalah
Un = n².
- Berdasarkan analisis, rumus suku ke-n untuk jumlah titik adalah
-
Menentukan Jumlah Titik pada Suku ke-10 (Bagian c):
- Gunakan rumus suku ke-n:
Un = n². - Untuk mencari jumlah titik pada suku ke-10, substitusikan
n = 10. - U10 = 10² = 100.
- Gunakan rumus suku ke-n:
Jawaban Soal 3:
a. Jumlah titik pada suku ke-5 adalah 25.
b. Rumus suku ke-n adalah Un = n².
c. Jumlah titik pada suku ke-10 adalah 100.
Contoh Soal 4: Pola Campuran atau Non-Linear
Perhatikan barisan bilangan berikut: 1, 4, 9, 16, 25, …
Tentukan:
a. Suku ke-6 dan suku ke-7.
b. Rumus suku ke-n (Un).
c. Suku ke-100.
Analisis dan Strategi Penyelesaian:
-
Mengidentifikasi Jenis Pola:
- Perhatikan selisih antar suku:
- 4 – 1 = 3
- 9 – 4 = 5
- 16 – 9 = 7
- 25 – 16 = 9
- Selisihnya tidak konstan (3, 5, 7, 9, …). Ini bukan pola aritmetika murni.
- Perhatikan selisih dari selisih (selisih tingkat kedua):
- 5 – 3 = 2
- 7 – 5 = 2
- 9 – 7 = 2
- Karena selisih tingkat keduanya konstan (yaitu 2), maka ini adalah pola kuadratik.
- Alternatif lain yang lebih cepat jika Anda mengenali pola ini adalah bahwa suku-suku tersebut adalah bilangan kuadrat sempurna: 1², 2², 3², 4², 5², …
- Perhatikan selisih antar suku:
-
Menentukan Suku ke-6 dan Suku ke-7 (Bagian a):
- Menggunakan identifikasi pola bilangan kuadrat:
- Suku ke-6 (U6) = 6² = 36.
- Suku ke-7 (U7) = 7² = 49.
- Atau, jika melanjutkan selisih tingkat pertama: selisih berikutnya adalah 9 + 2 = 11, lalu 11 + 2 = 13.
- U6 = 25 + 11 = 36.
- U7 = 36 + 13 = 49.
- Menggunakan identifikasi pola bilangan kuadrat:
-
Menentukan Rumus Suku ke-n (Bagian b):
- Berdasarkan identifikasi bahwa suku-suku tersebut adalah kuadrat dari nomor urutnya, maka rumus suku ke-n adalah
Un = n². - (Untuk pemahaman yang lebih mendalam, pola kuadratik dapat dirumuskan secara umum sebagai
Un = An² + Bn + C. Dengan mensubstitusikan beberapa suku pertama, kita bisa menemukan nilai A, B, dan C. Dalam kasus ini, A=1, B=0, C=0, sehingga menjadiUn = n²).
- Berdasarkan identifikasi bahwa suku-suku tersebut adalah kuadrat dari nomor urutnya, maka rumus suku ke-n adalah
-
Menentukan Suku ke-100 (Bagian c):
- Gunakan rumus suku ke-n:
Un = n². - Untuk mencari suku ke-100, substitusikan
n = 100. - U100 = 100² = 10.000.
- Gunakan rumus suku ke-n:
Jawaban Soal 4:
a. Suku ke-6 adalah 36, suku ke-7 adalah 49.
b. Rumus suku ke-n adalah Un = n².
c. Suku ke-100 adalah 10.000.
Contoh Soal 5: Menggunakan Konteks Cerita
Seorang petani menanam bibit pohon mangga. Pada bulan pertama, ia menanam 5 bibit. Setiap bulan berikutnya, ia menanam bibit dua kali lipat dari jumlah bibit yang ditanam pada bulan sebelumnya, ditambah 3 bibit lagi.
a. Berapa bibit yang ditanam pada bulan ke-3?
b. Tuliskan rumus untuk jumlah bibit yang ditanam pada bulan ke-n (Bn).
c. Berapa total bibit yang ditanam petani pada bulan ke-5?
Analisis dan Strategi Penyelesaian:
-
Mengidentifikasi Pola:
- Bulan 1 (n=1): B1 = 5 bibit.
- Bulan 2 (n=2): "dua kali lipat dari bulan sebelumnya, ditambah 3".
- B2 = (2 B1) + 3 = (2 5) + 3 = 10 + 3 = 13 bibit.
- Bulan 3 (n=3):
- B3 = (2 B2) + 3 = (2 13) + 3 = 26 + 3 = 29 bibit.
-
Menentukan Bibit pada Bulan ke-3 (Bagian a):
- Sudah dihitung di atas, jumlah bibit pada bulan ke-3 adalah 29 bibit.
-
Menulis Rumus untuk Jumlah Bibit pada Bulan ke-n (Bagian b):
- Dari langkah-langkah sebelumnya, kita bisa melihat bahwa jumlah bibit pada bulan ke-n (Bn) bergantung pada jumlah bibit pada bulan sebelumnya (Bn-1). Hubungannya adalah:
Bn = 2 * Bn-1 + 3, dengan syaratB1 = 5.- Ini adalah relasi rekurensi. Untuk mendapatkan rumus eksplisit (Bn dalam bentuk n saja) memang membutuhkan pemahaman lebih lanjut, namun untuk kelas 8, memahami relasi rekurensi ini sudah cukup baik.
-
Menentukan Total Bibit yang Ditanam pada Bulan ke-5 (Bagian c):
- Kita perlu melanjutkan perhitungan:
- Bulan 4 (n=4): B4 = (2 B3) + 3 = (2 29) + 3 = 58 + 3 = 61 bibit.
- Bulan 5 (n=5): B5 = (2 B4) + 3 = (2 61) + 3 = 122 + 3 = 125 bibit.
- Kita perlu melanjutkan perhitungan:
Jawaban Soal 5:
a. Bibit yang ditanam pada bulan ke-3 adalah 29 bibit.
b. Rumusnya adalah Bn = 2 * Bn-1 + 3, dengan B1 = 5.
c. Total bibit yang ditanam petani pada bulan ke-5 adalah 125 bibit.
Tips Menguasai Pola Bilangan
- Pahami Konsep Dasar: Pastikan Anda benar-benar mengerti perbedaan antara pola aritmetika dan geometri, serta bagaimana mengidentifikasi suku pertama dan beda/rasio.
- Teliti dalam Menghitung: Kesalahan kecil dalam penjumlahan, pengurangan, perkalian, atau pembagian dapat menghasilkan jawaban yang salah. Periksa kembali perhitungan Anda.
- Perhatikan Pola Tingkat Lanjut: Jangan ragu untuk melihat selisih antar suku (selisih tingkat pertama), bahkan selisih dari selisih tersebut (selisih tingkat kedua) jika pola awal tidak terlihat jelas. Ini membantu mengidentifikasi pola kuadratik atau yang lebih kompleks.
- Hafalkan Rumus Dasar: Rumus suku ke-n untuk aritmetika (
Un = a + (n-1)b) dan geometri (Un = a * r^(n-1)) sangat penting. Latihlah diri Anda untuk dapat menggunakannya dengan cepat. - Gunakan Visualisasi: Untuk pola bilangan khusus seperti pola persegi, segitiga, atau pola dengan susunan benda, cobalah menggambarkannya. Ini sangat membantu memahami aturan pembentukannya.
- Latihan Soal Beragam: Semakin banyak jenis soal yang Anda kerjakan, semakin luas pemahaman Anda. Jangan hanya terpaku pada satu jenis pola.
- Cari Keterkaitan: Perhatikan bagaimana pola bilangan muncul dalam kehidupan nyata. Ini akan membuat belajar menjadi lebih menarik dan relevan.
- Diskusikan dengan Teman atau Guru: Jika ada soal yang sulit, jangan sungkan untuk bertanya dan berdiskusi. Belajar bersama seringkali lebih efektif.
Kesimpulan
Pola bilangan adalah kunci penting dalam membuka pintu pemahaman matematika yang lebih luas. Dengan mengenali jenis pola, mengidentifikasi aturan pembentukannya, dan menggunakan rumus yang tepat, Anda dapat menyelesaikan berbagai macam soal. Mulai dari pola aritmetika dan geometri yang mendasar hingga pola bilangan khusus yang lebih menarik, setiap jenis pola mengajarkan cara berpikir logis dan analitis. Teruslah berlatih, jangan takut salah, dan nikmati proses menjelajahi dunia pola bilangan yang penuh keindahan dan keteraturan!