Pola bilangan adalah salah satu konsep fundamental dalam matematika yang seringkali menjadi pintu gerbang untuk memahami berbagai topik yang lebih kompleks. Di kelas 8 semester 1 Kurikulum 2013, pemahaman mendalam tentang pola bilangan menjadi krusial, tidak hanya untuk menjawab soal-soal ujian, tetapi juga untuk membangun fondasi berpikir logis dan analitis. Artikel ini akan mengupas tuntas contoh-contoh soal pola bilangan yang umum dijumpai, lengkap dengan penjelasan mendalam, strategi penyelesaian, dan tips agar Anda dapat menguasainya dengan percaya diri.
Mengapa Pola Bilangan Penting?
Sebelum kita menyelami contoh soal, mari kita pahami mengapa pola bilangan begitu penting. Pola bilangan adalah urutan angka yang memiliki aturan tertentu. Dengan mengidentifikasi aturan ini, kita dapat memprediksi angka selanjutnya dalam urutan, menemukan suku ke-n, bahkan merumuskan generalisasi matematis. Kemampuan ini melatih otak kita untuk melihat keteraturan, menganalisis data, dan membuat prediksi yang akurat. Dalam kehidupan sehari-hari, konsep pola bilangan hadir di mana-mana, mulai dari penanggalan, jadwal kereta api, hingga struktur kristal dalam sains.
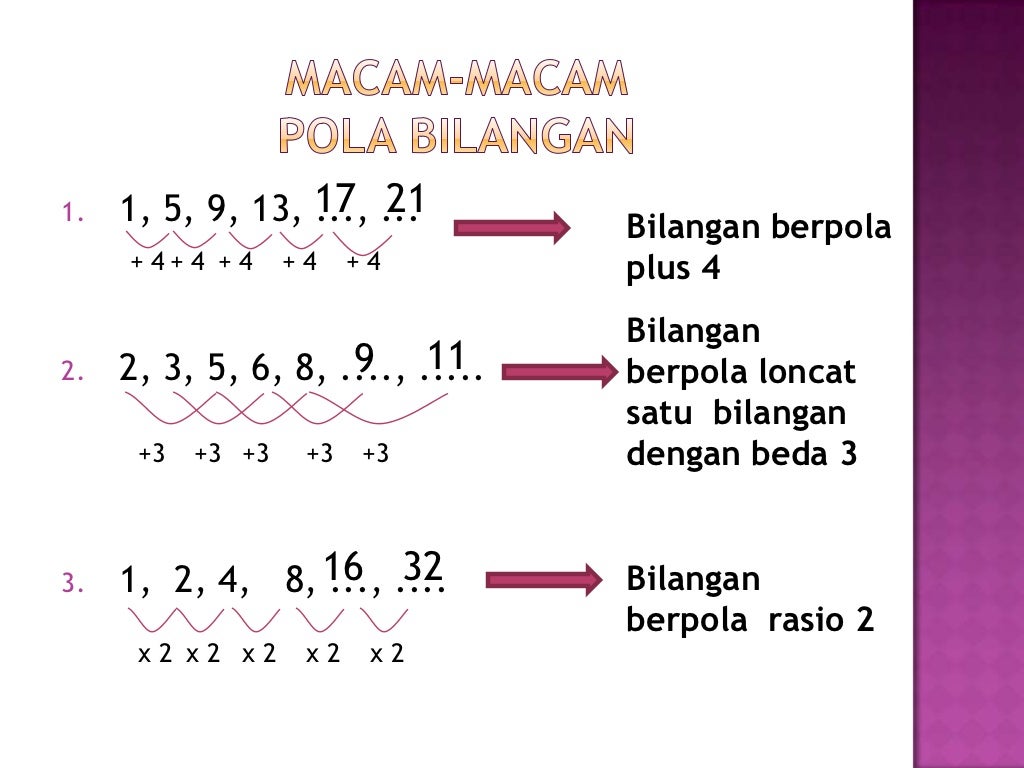
Jenis-Jenis Pola Bilangan yang Sering Muncul
Di kelas 8, kita akan bertemu dengan beberapa jenis pola bilangan yang umum, antara lain:
- Pola Aritmetika: Urutan bilangan di mana selisih antara dua suku berurutan selalu tetap. Selisih ini disebut beda.
- Pola Geometri: Urutan bilangan di mana perbandingan antara dua suku berurutan selalu tetap. Perbandingan ini disebut rasio.
- Pola Bilangan Khusus: Pola bilangan yang memiliki aturan unik dan seringkali dikaitkan dengan bentuk geometris atau konsep matematika lainnya, seperti pola bilangan persegi, persegi panjang, segitiga, Fibonacci, dan lain-lain.
Mari kita mulai dengan contoh-contoh soal yang mencakup jenis-jenis pola bilangan ini.
Contoh Soal 1: Identifikasi Pola dan Suku Berikutnya (Pola Aritmetika Sederhana)
Soal: Tentukan tiga suku berikutnya dari barisan bilangan berikut: 3, 7, 11, 15, …
Pembahasan:
Langkah pertama dalam memecahkan soal pola bilangan adalah mengidentifikasi aturan yang menghubungkan setiap suku. Mari kita periksa selisih antara suku-suku yang berurutan:
- Suku ke-2 – Suku ke-1 = 7 – 3 = 4
- Suku ke-3 – Suku ke-2 = 11 – 7 = 4
- Suku ke-4 – Suku ke-3 = 15 – 11 = 4
Terlihat bahwa selisih antara setiap suku yang berurutan adalah konstan, yaitu 4. Ini menandakan bahwa barisan bilangan ini adalah barisan aritmetika dengan beda ($b$) sebesar 4.
Untuk menemukan tiga suku berikutnya, kita cukup menambahkan beda (4) pada suku terakhir yang diketahui (15):
- Suku ke-5 = Suku ke-4 + b = 15 + 4 = 19
- Suku ke-6 = Suku ke-5 + b = 19 + 4 = 23
- Suku ke-7 = Suku ke-6 + b = 23 + 4 = 27
Jawaban: Tiga suku berikutnya dari barisan bilangan tersebut adalah 19, 23, dan 27.
Contoh Soal 2: Mencari Suku ke-n (Pola Aritmetika dengan Rumus)
Soal: Dalam sebuah barisan aritmetika, suku pertama adalah 5 dan bedanya adalah 3. Tentukan suku ke-20 dari barisan tersebut.
Pembahasan:
Untuk barisan aritmetika, kita memiliki rumus umum untuk mencari suku ke-n ($U_n$):
$U_n = a + (n-1)b$
Di mana:
- $U_n$ adalah suku ke-n
- $a$ adalah suku pertama
- $n$ adalah nomor urut suku yang ingin dicari
- $b$ adalah beda barisan
Dari soal, kita diketahui:
- $a = 5$ (suku pertama)
- $b = 3$ (beda)
- $n = 20$ (kita ingin mencari suku ke-20)
Sekarang, kita substitusikan nilai-nilai ini ke dalam rumus:
$U20 = 5 + (20-1) times 3$
$U20 = 5 + (19) times 3$
$U20 = 5 + 57$
$U20 = 62$
Jawaban: Suku ke-20 dari barisan aritmetika tersebut adalah 62.
Contoh Soal 3: Identifikasi Pola dan Suku Berikutnya (Pola Geometri Sederhana)
Soal: Tentukan tiga suku berikutnya dari barisan bilangan berikut: 2, 6, 18, 54, …
Pembahasan:
Sama seperti sebelumnya, kita mulai dengan mencari hubungan antar suku. Kali ini, kita akan mencoba membagi suku yang berurutan:
- Suku ke-2 / Suku ke-1 = 6 / 2 = 3
- Suku ke-3 / Suku ke-2 = 18 / 6 = 3
- Suku ke-4 / Suku ke-3 = 54 / 18 = 3
Terlihat bahwa perbandingan antara setiap suku yang berurutan adalah konstan, yaitu 3. Ini menandakan bahwa barisan bilangan ini adalah barisan geometri dengan rasio ($r$) sebesar 3.
Untuk menemukan tiga suku berikutnya, kita cukup mengalikan suku terakhir yang diketahui (54) dengan rasio (3):
- Suku ke-5 = Suku ke-4 $times$ r = 54 $times$ 3 = 162
- Suku ke-6 = Suku ke-5 $times$ r = 162 $times$ 3 = 486
- Suku ke-7 = Suku ke-6 $times$ r = 486 $times$ 3 = 1458
Jawaban: Tiga suku berikutnya dari barisan bilangan tersebut adalah 162, 486, dan 1458.
Contoh Soal 4: Mencari Suku ke-n (Pola Geometri dengan Rumus)
Soal: Dalam sebuah barisan geometri, suku pertama adalah 4 dan rasionya adalah 2. Tentukan suku ke-8 dari barisan tersebut.
Pembahasan:
Rumus umum untuk mencari suku ke-n ($U_n$) dalam barisan geometri adalah:
$U_n = a times r^(n-1)$
Di mana:
- $U_n$ adalah suku ke-n
- $a$ adalah suku pertama
- $n$ adalah nomor urut suku yang ingin dicari
- $r$ adalah rasio barisan
Dari soal, kita diketahui:
- $a = 4$ (suku pertama)
- $r = 2$ (rasio)
- $n = 8$ (kita ingin mencari suku ke-8)
Substitusikan nilai-nilai tersebut ke dalam rumus:
$U_8 = 4 times 2^(8-1)$
$U_8 = 4 times 2^7$
Kita perlu menghitung $2^7$:
$2^1 = 2$
$2^2 = 4$
$2^3 = 8$
$2^4 = 16$
$2^5 = 32$
$2^6 = 64$
$2^7 = 128$
Maka:
$U_8 = 4 times 128$
$U_8 = 512$
Jawaban: Suku ke-8 dari barisan geometri tersebut adalah 512.
Contoh Soal 5: Pola Bilangan Persegi
Soal: Perhatikan susunan titik berikut:
- Titik pertama: . (1 titik)
- Titik kedua:
. .
. . (4 titik) - Titik ketiga:
. . .
. . .
. . . (9 titik)
Berapa banyak titik pada susunan ke-5?
Pembahasan:
Mari kita amati jumlah titik pada setiap susunan: 1, 4, 9.
- Susunan ke-1: 1 titik
- Susunan ke-2: 4 titik
- Susunan ke-3: 9 titik
Kita dapat melihat bahwa jumlah titik pada setiap susunan adalah kuadrat dari nomor urut susunan tersebut:
- Susunan ke-1: $1^2 = 1$
- Susunan ke-2: $2^2 = 4$
- Susunan ke-3: $3^2 = 9$
Ini adalah pola bilangan persegi. Untuk mencari banyak titik pada susunan ke-5, kita cukup menghitung kuadrat dari 5:
Jumlah titik pada susunan ke-5 = $5^2 = 25$
Jawaban: Banyak titik pada susunan ke-5 adalah 25.
Contoh Soal 6: Pola Bilangan Persegi Panjang
Soal: Perhatikan susunan titik berikut yang membentuk persegi panjang:
- Susunan ke-1: . . (2 titik)
- Susunan ke-2:
. . .
. . . (6 titik) - Susunan ke-3:
. . . .
. . . .
. . . . (12 titik)
Berapa banyak titik pada susunan ke-4?
Pembahasan:
Jumlah titik pada setiap susunan adalah: 2, 6, 12.
Mari kita coba mencari polanya. Kita bisa perhatikan bahwa jumlah titik pada susunan ke-$n$ adalah hasil perkalian $n$ dengan $(n+1)$.
- Susunan ke-1: $1 times (1+1) = 1 times 2 = 2$
- Susunan ke-2: $2 times (2+1) = 2 times 3 = 6$
- Susunan ke-3: $3 times (3+1) = 3 times 4 = 12$
Ini adalah pola bilangan persegi panjang. Untuk mencari banyak titik pada susunan ke-4, kita gunakan rumus $n times (n+1)$ dengan $n=4$:
Jumlah titik pada susunan ke-4 = $4 times (4+1) = 4 times 5 = 20$
Jawaban: Banyak titik pada susunan ke-4 adalah 20.
Contoh Soal 7: Pola Bilangan Segitiga
Soal: Perhatikan susunan titik berikut yang membentuk segitiga:
- Susunan ke-1: . (1 titik)
- Susunan ke-2:
.
. . (3 titik) - Susunan ke-3:
.
. .
. . . (6 titik)
Berapa banyak titik pada susunan ke-5?
Pembahasan:
Jumlah titik pada setiap susunan adalah: 1, 3, 6.
Mari kita analisis polanya. Kita bisa melihat bahwa jumlah titik pada susunan ke-$n$ adalah jumlah dari bilangan asli dari 1 hingga $n$.
- Susunan ke-1: 1
- Susunan ke-2: 1 + 2 = 3
- Susunan ke-3: 1 + 2 + 3 = 6
Ini adalah pola bilangan segitiga. Rumus umum untuk mencari suku ke-n pola bilangan segitiga adalah:
$S_n = fracn(n+1)2$
Untuk mencari banyak titik pada susunan ke-5, kita gunakan rumus dengan $n=5$:
$S_5 = frac5(5+1)2$
$S_5 = frac5 times 62$
$S_5 = frac302$
$S_5 = 15$
Jawaban: Banyak titik pada susunan ke-5 adalah 15.
Contoh Soal 8: Pola Bilangan Fibonacci
Soal: Tentukan dua suku berikutnya dari barisan bilangan Fibonacci: 1, 1, 2, 3, 5, 8, …
Pembahasan:
Barisan Fibonacci adalah barisan bilangan di mana setiap suku setelah suku kedua adalah jumlah dari dua suku sebelumnya.
Mari kita periksa aturan ini pada barisan yang diberikan:
- Suku ke-3 = Suku ke-1 + Suku ke-2 = 1 + 1 = 2 (Benar)
- Suku ke-4 = Suku ke-2 + Suku ke-3 = 1 + 2 = 3 (Benar)
- Suku ke-5 = Suku ke-3 + Suku ke-4 = 2 + 3 = 5 (Benar)
- Suku ke-6 = Suku ke-4 + Suku ke-5 = 3 + 5 = 8 (Benar)
Untuk menemukan dua suku berikutnya, kita lanjutkan aturan ini:
- Suku ke-7 = Suku ke-5 + Suku ke-6 = 5 + 8 = 13
- Suku ke-8 = Suku ke-6 + Suku ke-7 = 8 + 13 = 21
Jawaban: Dua suku berikutnya dari barisan bilangan Fibonacci adalah 13 dan 21.
Strategi Jitu Menguasai Pola Bilangan
- Teliti dan Sabar: Jangan terburu-buru dalam mengidentifikasi pola. Perhatikan setiap angka dengan cermat.
- Coba Berbagai Kemungkinan: Jika pola aritmetika tidak ditemukan, coba cari pola geometri. Jika keduanya tidak cocok, periksa apakah itu pola bilangan khusus.
- Periksa Selisih dan Perbandingan: Ini adalah langkah awal yang paling umum untuk pola aritmetika dan geometri.
- Perhatikan Bentuk Visual: Untuk pola bilangan khusus seperti persegi, persegi panjang, atau segitiga, gambarlah susunan titiknya untuk membantu visualisasi.
- Hafalkan Rumus Dasar: Rumus suku ke-n untuk barisan aritmetika dan geometri, serta rumus untuk pola bilangan khusus yang sering muncul, sangat membantu.
- Latihan, Latihan, Latihan: Semakin banyak Anda berlatih berbagai jenis soal, semakin terasah kemampuan Anda dalam mengenali pola.
- Pahami Konteks Soal: Terkadang, konteks soal (misalnya, cerita tentang pertumbuhan bakteri atau penyebaran informasi) dapat memberikan petunjuk tentang jenis pola yang digunakan.
Kesimpulan
Memahami pola bilangan bukan sekadar menghafal rumus, tetapi lebih kepada mengasah kemampuan berpikir logis dan analitis. Dengan menguasai berbagai jenis pola bilangan, termasuk aritmetika, geometri, dan pola-pola khusus, serta menerapkan strategi penyelesaian yang tepat, siswa kelas 8 semester 1 dapat menghadapi soal-soal matematika dengan lebih percaya diri. Ingatlah bahwa latihan yang konsisten adalah kunci utama untuk meraih kesuksesan dalam menguasai materi ini. Teruslah bereksplorasi, jangan ragu untuk mencoba berbagai pendekatan, dan nikmati keindahan keteraturan yang ditawarkan oleh dunia pola bilangan!



